Les instabilités du PMO: de la résonance cohérente au chaos
Modèle en propagation
Warning: include(menuinst.inc.php): failed to open stream: No such file or directory in /var/www/html/rech_instmep.php on line 28
Warning: include(): Failed opening 'menuinst.inc.php' for inclusion (include_path='.:/usr/local/lib/php') in /var/www/html/rech_instmep.php on line 28
Dans ce modèle, on écrit FT en fonction de I1, I2 et I3:
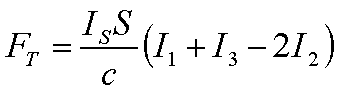
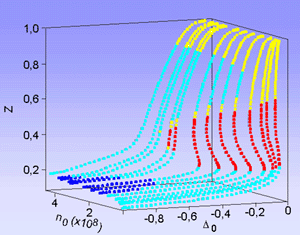
Fig. 11: cliquez sur l'image pour l'agrandir
À partir des équations de la matrice densité, on écrit les équations de propagation des faisceaux aller et retour. On introduit ensuite une densité atomique constante r qui permet de déduire la relation entre I1, I2 et I3, ainsi que la taille S du piège.
Dans l’espace des phases, la forme des solutions stationnaires est similaire à celle obtenue avec le modèle global, ainsi qu'on peut le voir sur la figure 11, où les couleurs codent la nature du point fixe: noeud stable, foyer stable, noeud selle (instable) ou foyer selle (instable).
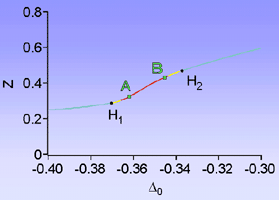
Fig. 12: cliquez sur l'image pour l'agrandir
Au voisinage de la zone bistable, il existe une zone instable apparaissant à travers deux bifurcations de Hopf (H1 et H2 sur le fig. 12)


